Using of Stability Map function
In this tutorial, we continue working on the schema created during the previous tutorial.
As we are building a V-shaped cavity, the schema includes inclined spherical mirror M1 that has different matrices for tangential and sagittal planes. Note, the mirror displayed a bit turned around on the layout to emphasize the beam falls on the element at an angle.
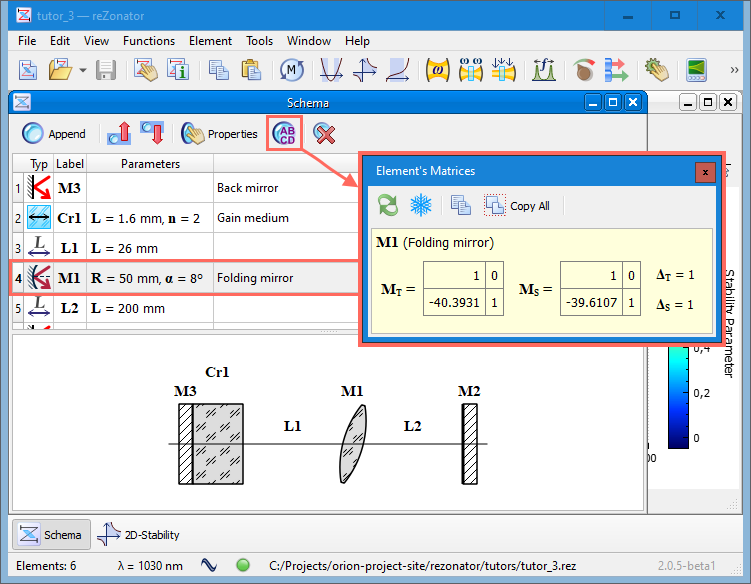
It means the stability parameter is also different for working planes. 2D Stability Map can display only one plane at the time; if we switch between planes, we can see that picture shifts. So it's not entirely clear if values for L1 and L2 those we selected provide the real stable operation. Tangential and sagittal planes are independent only mathematically, but physically they are projections of the same system, and the stability must be achieved for both of them.
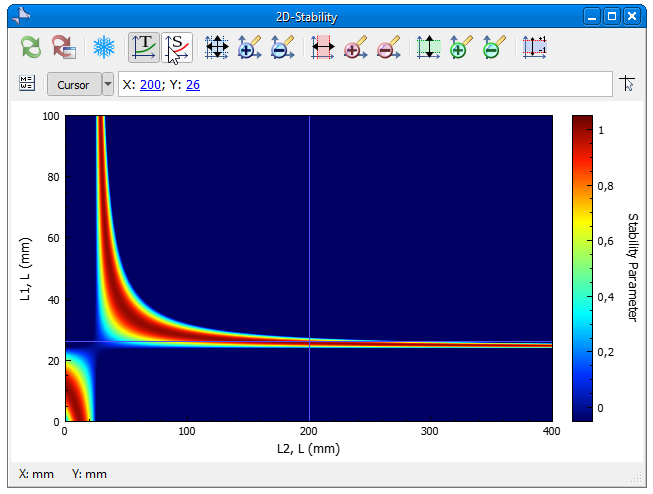
Version 1
Version 1 shows contour lines for both T and S planes at the same time, but it doesn't add a much because it's hard to distinguish if the current point falls into the stable region in both planes or not.
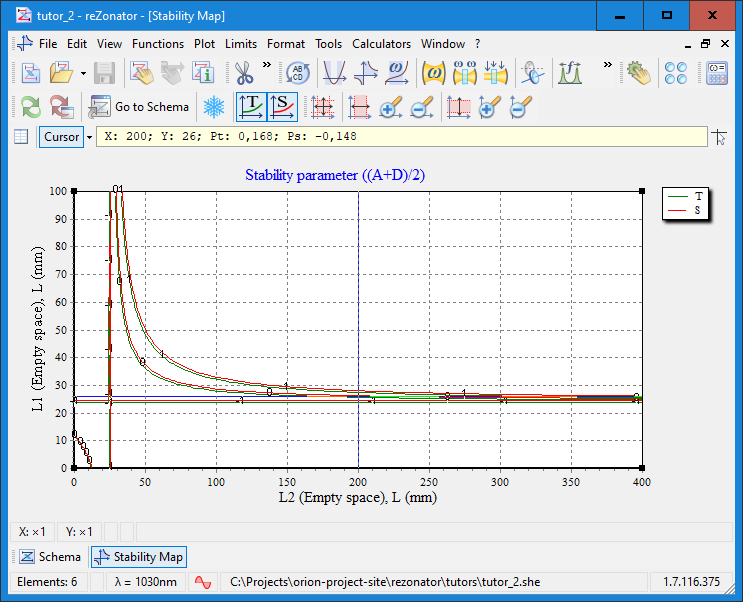
That's when the Stability Map function comes into play.
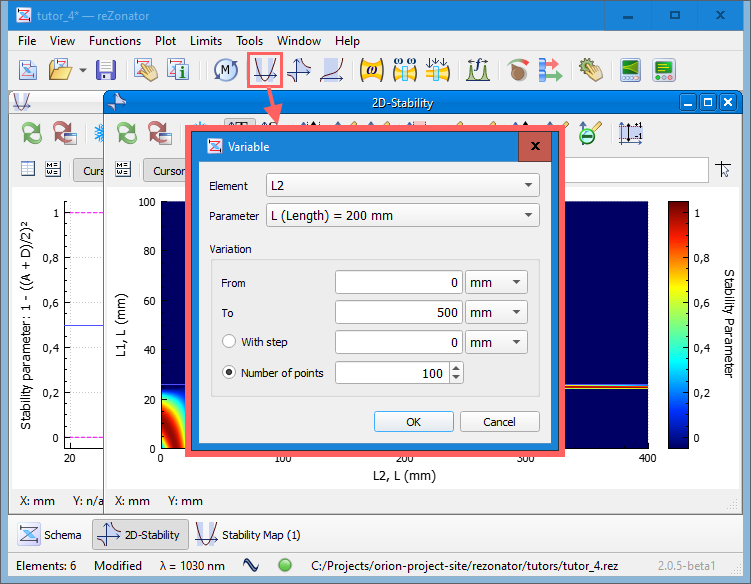
Since we know that with L2 = 200mm, the stability achieved when L1 is something about 26mm, we can refine the value for L1. Use the toolbar button or the menu "Function -> Stability Map...". We can variate L1 around the current value and see how it affects stability.
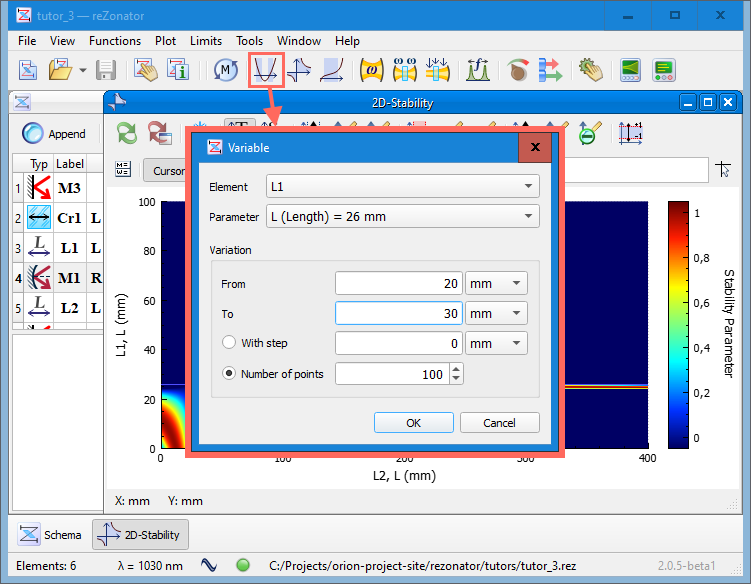
In general, stability graphs are smooth, so there is no need to use a large number of points for them. The default number is 100, and it's almost always enough.
Similar to the 2D Stability Map function, this function supports different modes of calculation of the stability parameter. Hit the small button near the "Cursor" button to open the left panel to switch between calculation modes.
Use the commands "Limits -> Y-axis to Stability Range" or the respective toolbar button to show only a substantial range of stability parameter values. Boundaries of this range depend on the calculation mode and marked by purple horizontal lines.
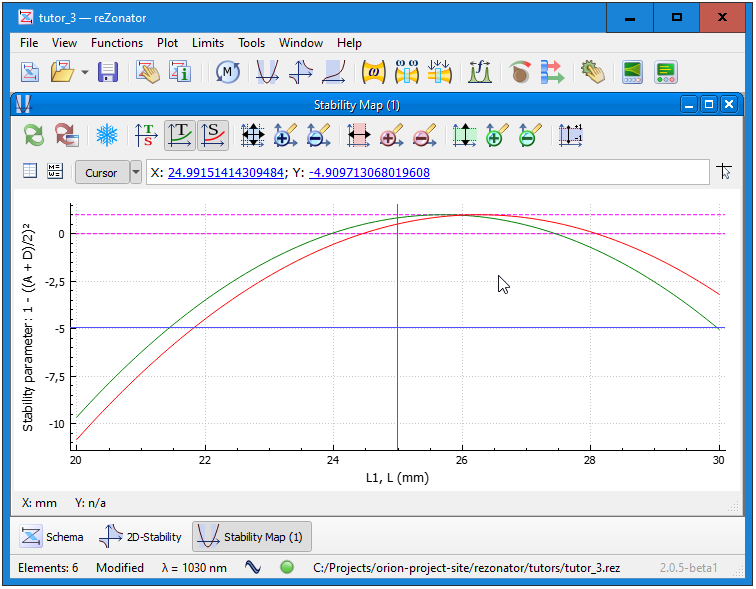
We can see that the stable operation can be achieved with L1 magnitudes between L1min ≈ 24.5mm and L1max ≈ 27.5mm. When L1 is within this diapason, both graphs for T and S planes are inside of the stable range marked by purple lines.
Also, we can see that our current value L1 = 26mm falls entirely in the middle of the stability range. Is it acceptable or not depends on the purpose of the designed resonator. It is suitable for stable continuous laser operation. Still, if one plans to have a mode-locking regime, it's worth to try shifting the system closer to one of the stability edges.
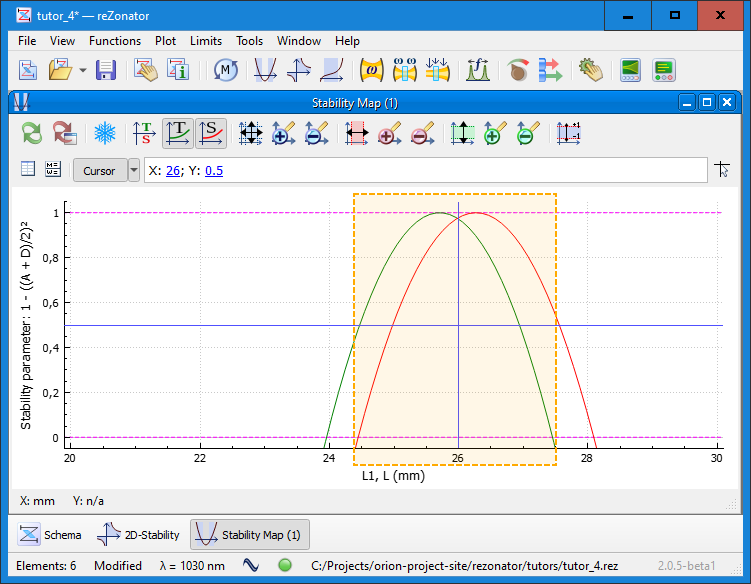
Similarly, we can check the system stability regarding changes of L2, having fixed L1. 2D Stability Map already shows us that the stability is much more tolerant of changes of L2 when L1 = 26mm and around, so we can boldly use a wide variation range.
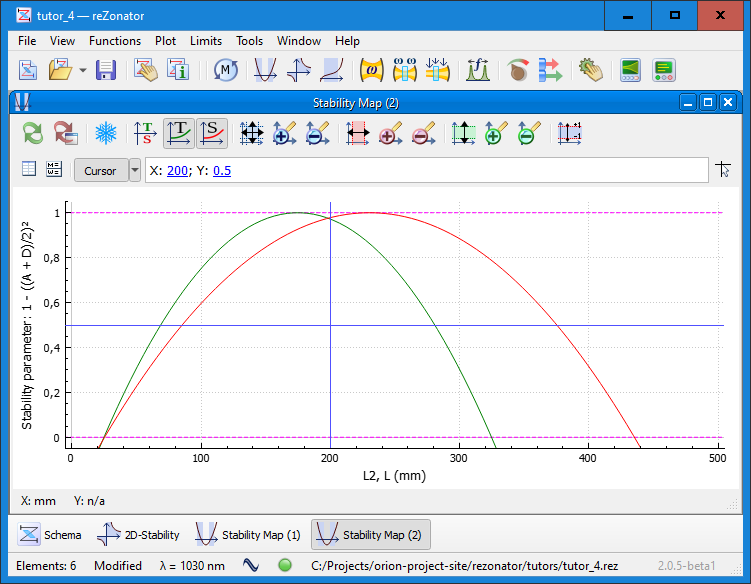
And again, we can see that the current magnitude L2 = 200mm falls in the middle of the stability range, so it's good enough. What is interesting, T and S graphs diverge quite far from each other. It gives the upper stability boundary L2max ≈ 325mm. However, even within this limit, the S graph passes rather upper than the T graph. It means that the beam shape will be somewhat uneven by these L2 values.
Download schema file for version 1, for version 2.